「私、文系だから、数学は勉強しても意味がない！」

「数列も2次関数も、難しいし、無意味だ！」

って感じていませんか？

たしかに大人になってから、「高校で習った数学を１回も使ったことがない」という人もいるようです。

そこで！ 理系新人編集者ワイワイ（僕）は考えた！

「数学はキミの生活にも役立つよ！」って高校生のキミに伝えたい！

今回は、「数学を知らないと、将来お金で損するかも...！」という話を、数学Bの「数列」の単元を使って、紹介していきます。

図解でわかりやすく書いたので、まだ数列を習っていない人も、数学がニガテな人も、ぜひ最後まで読んでみてください！

今回は「リボ払いの罠」を紹介していきます。

リボ払いとは？

テレビCMで「リボ払い」という言葉を聞いたことはありますか？

リボ払いとは、「クレジットカードなどで、一括払いではなくて、毎月同じ金額（例えば毎月1万円ずつ）支払っていく支払い方法」のことです。

「毎月のお支払い額が一定で、家計の管理に役立つ」などと紹介されています。

しかし、実はリボ払いには、かなり大きな罠が潜んでいるのです。

クイズ

いきなりですが、ここでクイズです！

以下のような状況を考えてみましょう。

こんなイメージをもった人も多いのではないでしょうか？

5.6年くらい、つまり社会人になるころには、支払いが完了すると、感じませんか？

ですが...

実際は、なんと23年もかかります...！！

18歳でPCを購入したとして、支払い終わるまでに41歳までかかってしまいます。

23年後のあなたは、そのPCをとっくに使っていないでしょう。

ずっと支払いが終わらない...。

数列で「リボ払いの罠」を解き明かす

今回は、数学Bの「数列」の知識を活用して、リボ払いについて向き合っていきましょう。

借金の残高と利息の関係を整理して、「毎月実質いくら借金が減るのか？」を考えよう

年利18 ％とは、

18 (%) ÷12ヶ月 = 1.5 (%)

で借金の残高（返済すべき金額）に対して、毎月1.5 %の利子がかかることを表します。

ちょっと難しく感じる金利の計算を、2つのステップに分けて考えてみます。

STEP (1) 3000円を支払う

まず、3000円を支払うことで、最初の借金の残高から、3000円を引きます。

すると、借金の残高が19万7000円となります。

STEP (2) 利息で、借金の残高が1.015倍になる

借金の残高が利息によって、1.015倍になります。

この流れをまとめると、以下のようになります。

最初の1か月目で、3000円支払っても、2955円が利子として追加されるので、実質、45円分しか支払いが進みません。

リボ払いでは、「せっかく支払ったのに、利子がかかるため、ほとんど支払いが進まない」という状態になるのです。

全然返済が進まない...！

一般項で表してみる

それでは、この流れを、「nか月目」として、当月と次の月の関係を表してみます。

「毎月3000円支払い、借金の残高に対して1.5 %の利息がかかる」というのを数式で表すと、こんな感じになります。

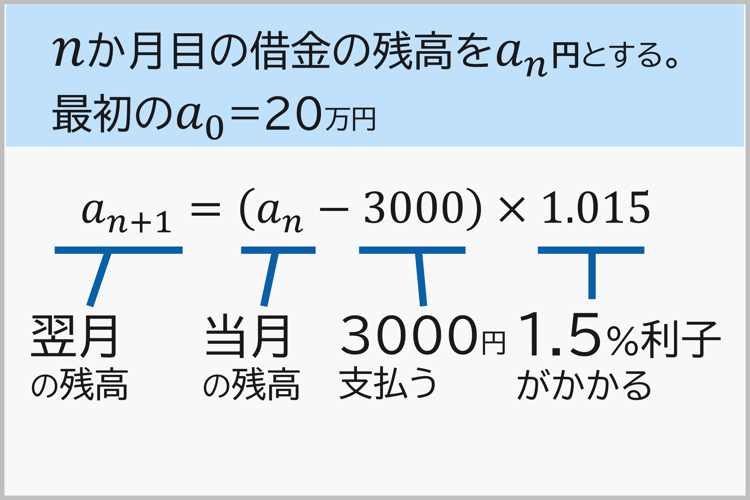
これは！

数列の漸化式です！

普段、数式だけを見ても意味がわからないと思っていても、

こうやって図や言葉で説明されると、わかりやすくなっていると感じませんか！？

返済状況を可視化してみよう

借金の残高の変化を、グラフにして見てみましょう

青線の分割払い（無利子）なら直線的ですが、

赤線のリボ払いは、同じ金額を払っていても、借金の残高が減るのがとてもゆっくりなのです！

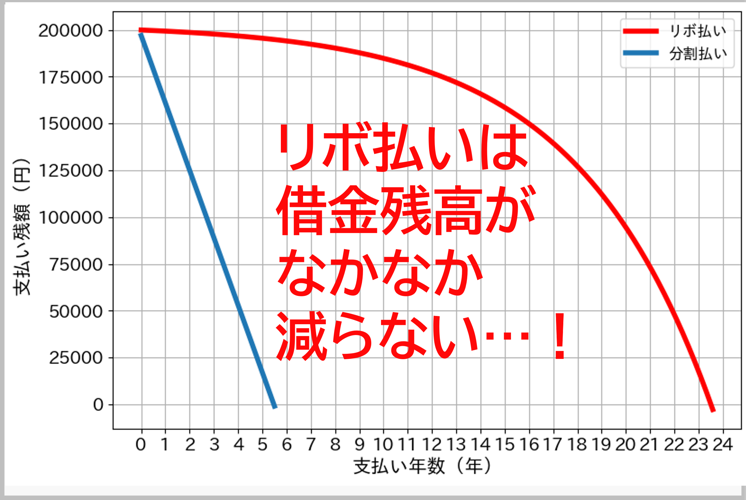
毎月コツコツ3000円を支払っても、ほとんどが利子として消えてしまいます。

リボ払いを選択すると、20万円のPCを買うために、なんと85万円も支払う必要があります。

リボ払いは「支払いがなかなか終わらない罠」があるので要注意です。

また、分割払いも、利子がかかることが多いので、注意しましょう。

金利や条件をよく確認して、自分で考えることが大切です。

数学の問題風に書いてみる

数学の問題のように書くと、こんな問題になります。

この問題を見ても、無味乾燥でつまらなく感じますが、実はリボ払いの支払い月数を求める問題になっているのです。

「なんのためにやっているのだろう...」と感じる数学の問題も、生活に置き換えれば、少しなじみが出てくるのではないでしょうか？

この記事の最後に式変形の途中式をSpecialおまけとして載せておきます！

数学好きの人は要チェック！

まとめ

数列の知識を知っていれば、「リボ払いの罠」に気づくことができるのです！

「数学は難しいし、勉強したくないな...」と感じているかもしれません。

数学を知っていると、「自分で考える」という力が身につきます。

数学がニガテと感じているあなたも、「数学って自分に役立つから勉強しよう！」と少しでも前向きに勉強に取り組んでもらえればうれしいです！

記事のコメント欄に、皆さんの「何のために勉強するのかわからない」と感じる分野を書いてくれるとうれしいです！

（数学に限らず、古文漢文・物理・化学・日本史など、なんでもOKです。）

「その科目、実はキミにも役立つよ！」という記事を書いてみます！

おまけの式変形

漸化式の一般項を求める式変形と、借金の返済が完了するまでの期間を求める過程を、簡単に解説します。

※この記事は、公開日時点の情報に基づいて制作しております。