「春休みにほんとはニガテをつぶしきりたかったけど、根が深すぎてやり残してしまった...」

と思っている人、結構いるんじゃないでしょうか。

特に、数学がニガテな人は、数学の問題を読んで理解するのに時間がかかり、解き始めるまでにエネルギーを消耗してぐったり。結局１問も解けなかった、という状態に陥っているのではないかと想像されます。

受験もそろそろ意識し始めなきゃと思い始めたときに、高１のニガテはなくしておきたい...！

そんな人のために、問題の内容をパッと理解できて、すぐに解き始めることができるようになる「テク」が詰まったテキストを、リクエストに応じてお届けします。

このテキストで数学のニガテをラクに解消しちゃいましょう！

そのテキストの中から２つの「テク」を特別にご紹介しちゃいます！

１．「楽がきテク」で、どう解くかがひとめでわかる！

例えば、２次関数のグラフのこんな問題。

どう解けばいいか、すぐにわかりますか？

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・

どう手をつけていいかわからなかった...。という人も安心してください。「楽がきテク」を使えば、解き方が一目でわかります。

「楽がきテク」を紹介！

上のような問題を見て、解き方が全く浮かばなかった人は、この「楽がきテク」を使いましょう。

グラフの「軸」が「定義域」の左にあるか、中なのか、右にあるのかで、最小となる位置が変わります。実際にグラフをかいて確認しましょう。

まず、「軸」が「定義域」の左にある場合の、最小の場所をチェック。ここでは、定義域の左端で最小になります。

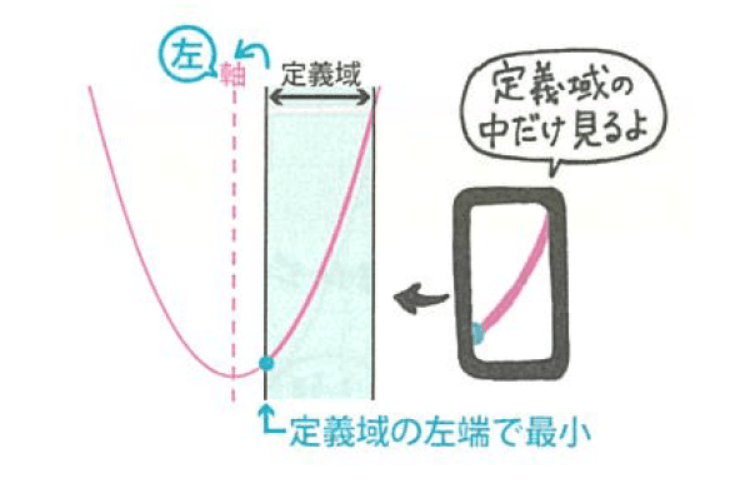
次に、「軸」が「定義域」の中にある場合の、最小の場所をチェック。この場合は、頂点で最小になりますね。

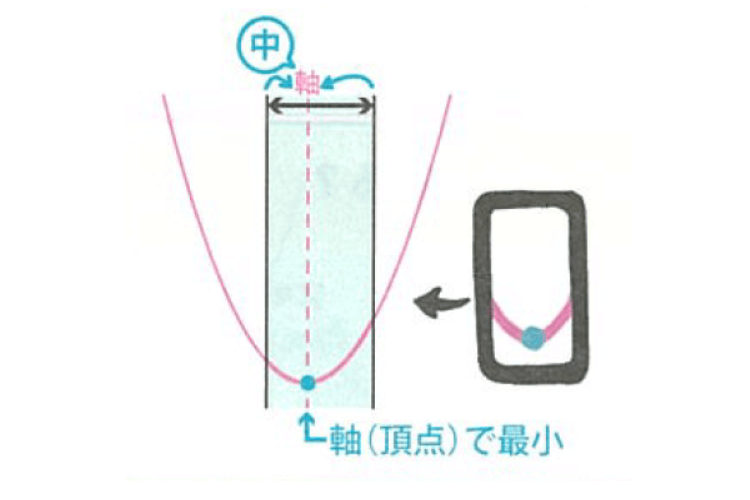
最後は、「軸」が「定義域」の右にある場合の最小の場所をチェック。この場合は、定義域の右端で最小になります。

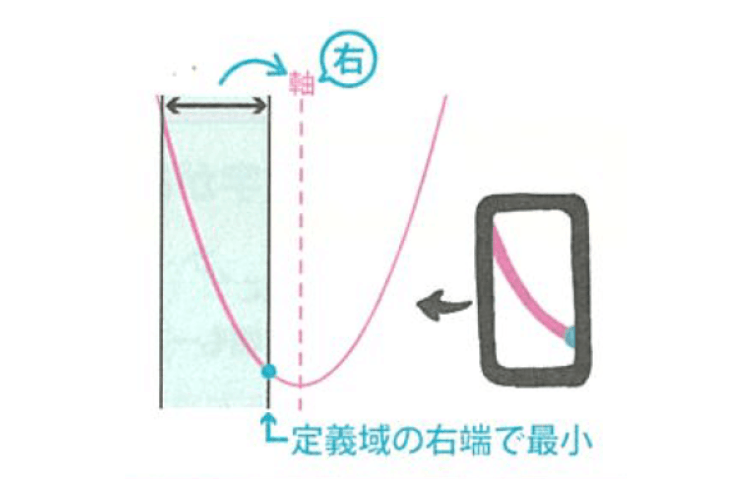
「楽がきテク」で注目すべき点が見えてきましたね！あとはこの３つを式で表せば、それがもう答えです。

この「楽がきテク」のようにグラフをかいて、最小の場所をおさえてから、問題を解き始めると、スムーズに答えを導き出せますね。

この教材なら、他の「楽がきテク」もわかります。今すぐリクエストして、取り組んでみてください！

>>「楽がきテク」の教材をリクエストする

２．「推理テク」で、瞬時に解法を思いつく！

例えば、この問題。どう解いていくか思いつきますか？

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・

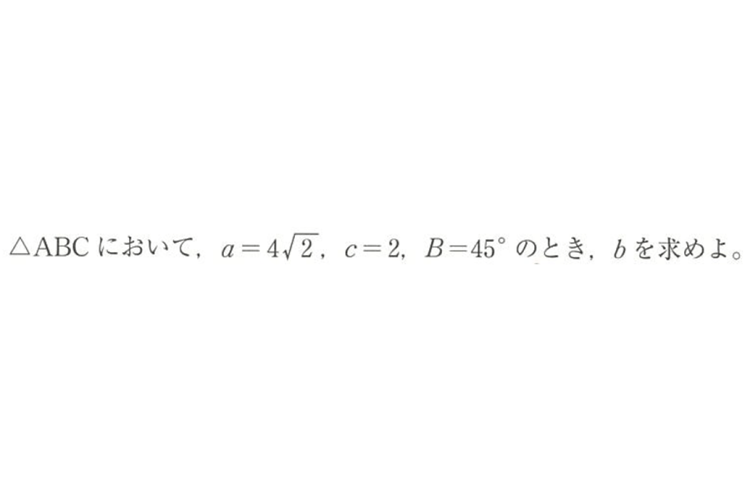
何から始めていいかわからなかった人も大丈夫！「推理テク」で、あっという間に、解法を思いつくことができるのです。

「推理テク」を紹介！

この問題の場合は、「2辺と1角」だから、余弦定理を使って解けることがわかります。

〇〇ときたら▲▲と覚えておけば、すぐに解法を思いつきますね。

この教材では、他の「推理テク」も掲載しています。今すぐリクエストして、瞬間で解法を思いつく体験をしてみませんか？

>>「推理テク」で解く教材をリクエストする

今まで、問題理解から答えまで、時間がかかっていた人も、「楽がきテク」や「推理テク」をマスターすれば、短時間で答えまで導けますよ！是非リクエストしてください。

※この記事は公開日時点の情報に基づいて制作しております。